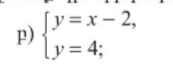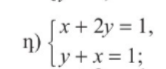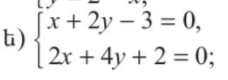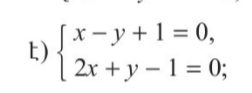Առաջադրանքներ
1․Հետևյալ համակարգը լուծիր գրաֆիկական եղանակով՝
{y=−3x
{y=3−4x
x1 = 0 y1 = 3 y2 = 0 x2 = 0,75
y=3−4x 2․Հետևյալ համակարգը լուծիր գրաֆիկական եղանակով՝
{y=1+x
{y=−5−x
x1 = 0 y1 = 1 y2 = 0 x2 = -1
y=1+x x1 = 0 y1 = -5 y2 = 0 x2 = -5
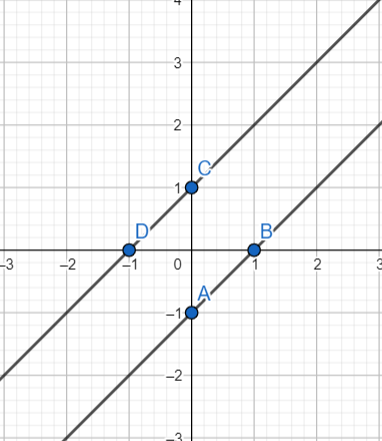
y=−5−x 3․Գրաֆիկորեն պարզիր, թե քանի՞ լուծում ունի համակարգը՝
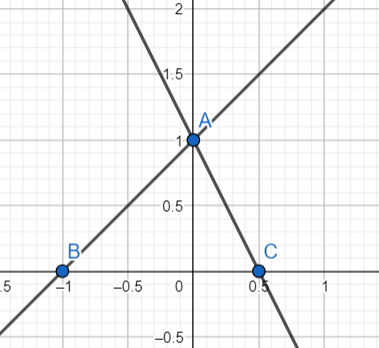
{y=x−1
{y=x+1
երկու լուծում մեկ լուծում ճիշտ պատասխանը բացակայում է լուծում չկա x1 = 0 y1 = -1 y2 = 0 x2 = 1
y=x−1 x1 = 0 y1 = 1 y2 = 0 x2 = -1
y=x+1 4․Գրաֆիկական եղանակով լուծիր համակարգը՝
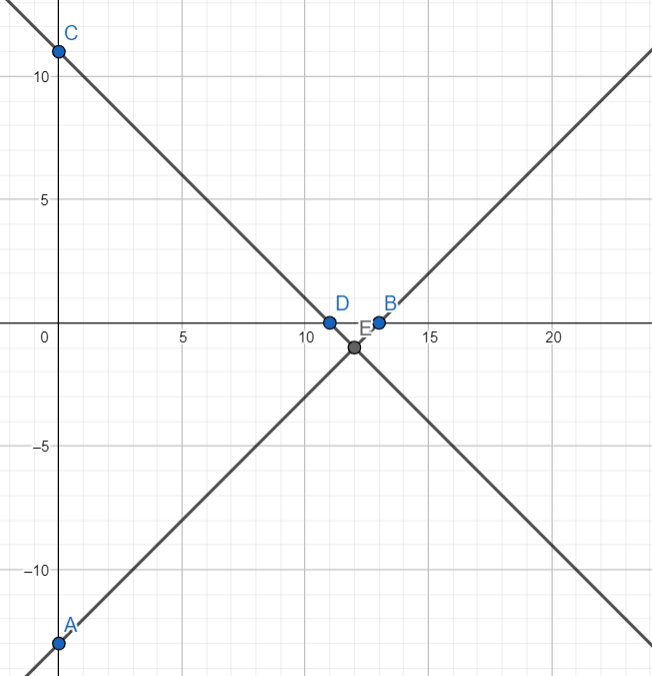
{y=x−13
{x+y=11
x1 = 0 y1 = -13 y2 = 0 x2 = 13
y=x−13 x1 = 0 y1 = 11 y2 = 0 x2 = 11
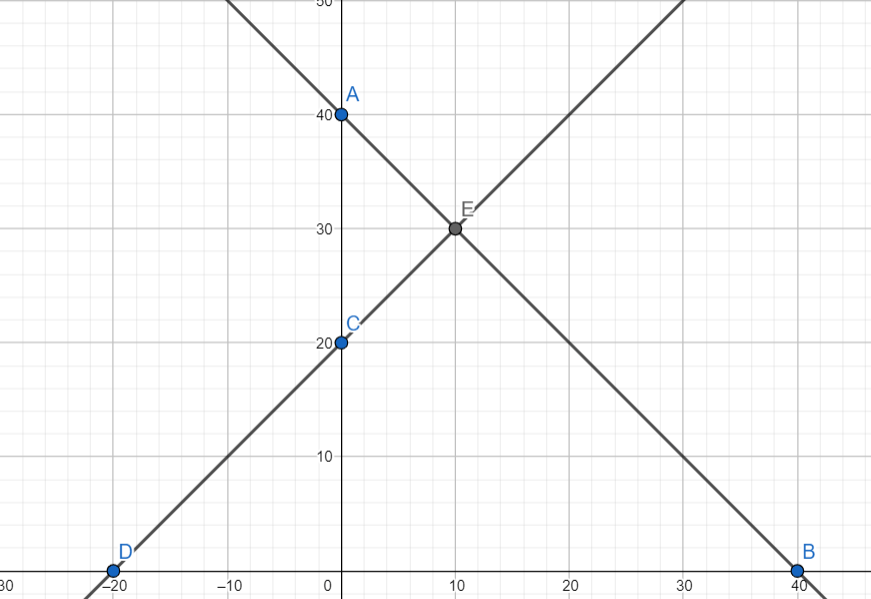
y = 11 — x 5․Գրաֆիկական եղանակով գտիր երկու այնպիսի թիվ, որոնց գումարը հավասար է 40-ի, իսկ տարբերությունը՝ 20-ի:
x1 = 0 y1 = 40 y2 = 0 x2 = 40
y = 40 — x x1 = 0 y1 = 20 y2 = 0 x2 = -20
y = 20 + x Պատ՝ 30, 10 6․Գտիր երկու թիվ, որոնց գումարը հավասար լինի 33-ի, իսկ տարբերությունը՝ 25-ի:
x1 = 0 y1 = 33 y2 = 0 x2 = 33
y = 33 — x x1 = 0 y1 = 20 y2 = 0 x2 = -20
y = 20 + x 26.5, 6.5 Դասագրքից՝ 68, 73
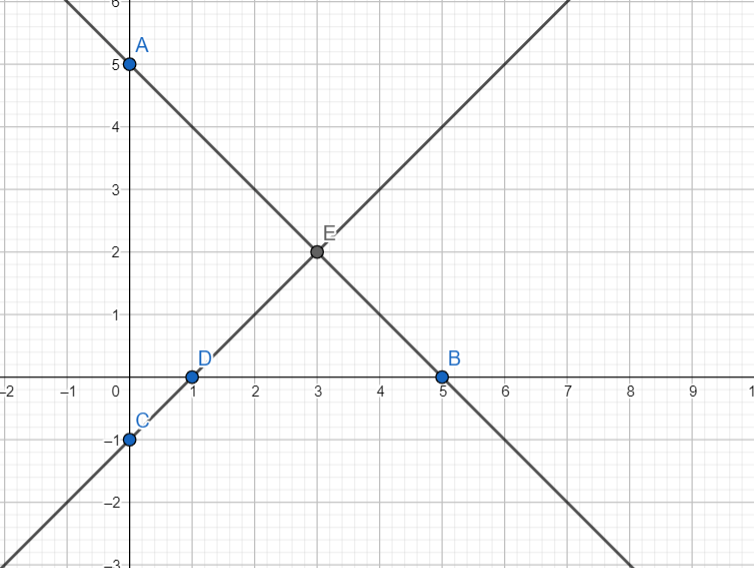
x1 = 0 y1 = 5 y2 = 0 x2 = 5
y = 5 — x x1 = 0 y1 = -1 y2 = 0 x2 = 1
y = x — 1 5 — x = x — 1
2x = 6
x = 3, y = 2
x1 = 0 y1 = -2 y2 = 0 x2 = 2
y = x — 2 x — 2 = 4
x = 6, y = 4
x1 = 0 y1 = -4 y2 = 0 x2 = 2
y = 2x — 4 x1 = 0 y1 = 2 y2 = 0 x2 = 2
y = 2 — x x = 2, y = 0
x1 = 0 y1 = 0,5 y2 = 0 x2 = 1
2y = 1 — x x1 = 0 y1 = 1 y2 = 0 x2 = 1
y = 1 — x x = 2, y = 0
x1 = 0 y1 = 1,5 y2 = 0 x2 = 3
2y = 3 — x x1 = 0 y1 = -0,5 y2 = 0 x2 = -1
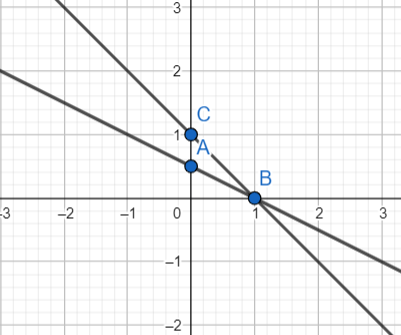
4y = -2 — 2x Լուծում չունի
x1 = 0 y1 = 0,5 y2 = 0 x2 = 1
2y = 1 — x x1 = 0 y1 = -4 y2 = 0 x2 = 4
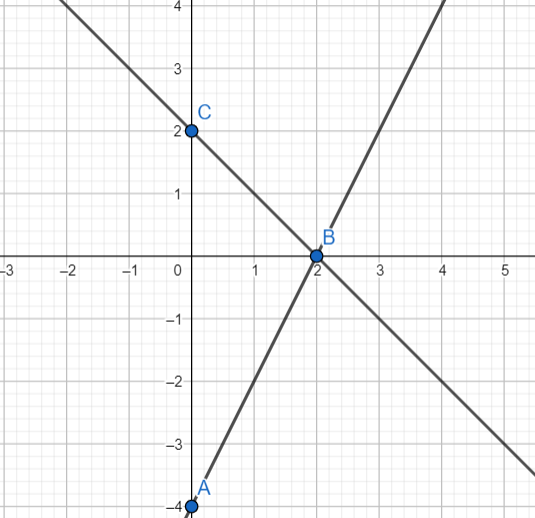
y = x — 4 x = 3, y = -1
x1 = 0 y1 = 1 y2 = 0 x2 = -1
y = x + 1 x1 = 0 y1 = 1 y2 = 0 x2 = 0,5
y = 1 — 2x x = 0, y = 1
x1 = 0 y1 = -3 y2 = 0 x2 = 0,4
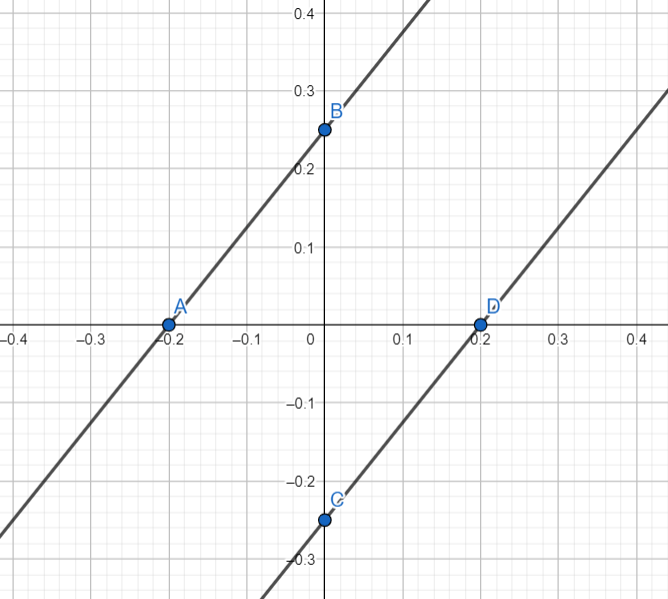
y = 7x — 3 x1 = 0 y1 = 2,5 y2 = 0 x2 = 0,5
2y = 14x + 5 Լուծում չունի
x1 = 0 y1 = 1 y2 = 0 x2 = 0,3
y = 1 — 3x x1 = 0 y1 = 1 y2 = 0 x2 = 0,3
2y = 2 — 6x (x:y)
x1 = 0 y1 = -2 y2 = 0 x2 = 2
y = x — 2 x1 = 0 y1 = 2 y2 = 0 x2 = -2
y = 2 + x Լուծում չունի
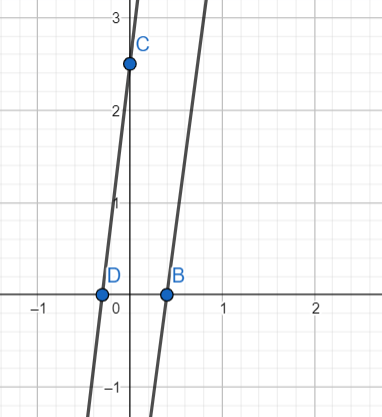
x1 = 0 y1 = 0,25 y2 = 0 x2 = 0,2
4y = 5x — 1 x1 = 0 y1 = 0,25 y2 = 0 x2 = -0,2
16y = 20x + 4 Լուծում չունի
x1 = 0 y1 = 1,5 y2 = 0 x2 = 3
2y = 3 — x x1 = 0 y1 = 2 y2 = 0 x2 = 4
y = 2 — 1/2x Լուծում չունի