Դասարանական և Տնային աշխատանք (Երկրաչափություն)

AB = A1B1

BC = B1C1

< B = <B1

Ըստ եռանկյան առաջին հայտանիշի, այդ երկու եռանկյունները իրար հավասար են։

<DCB = <D1C1B1

<B = <B1

BC = B1C1

եռանկյունները հավասար են, ըստ երկրորդ հայտանիշի

AB = A1B1

AC = A1C1

BC = B1C1

<B = <B1

<A = <A1

<C = <C1

Ըստ եռանկյան երկրորդ հայտանիշի եռանկյունները հավասար են

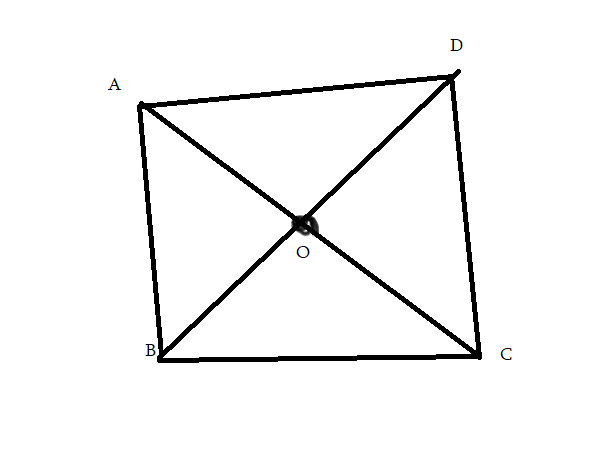
<BCO = <DAO

O միջնակետ

AO = OC

<C = <A

Ըստ եռանկյան երկրորդ հայտանիշի եռանկյունները հավսար են

եռանկյուն ACB = եռանկյուն ACD

Պարզեցինք, որ AB = DC, BC = AD

Այսքան պայմաններից հետո կարելի է ասել, որ այդ երկու եռանկյունները իրար հավասար են։

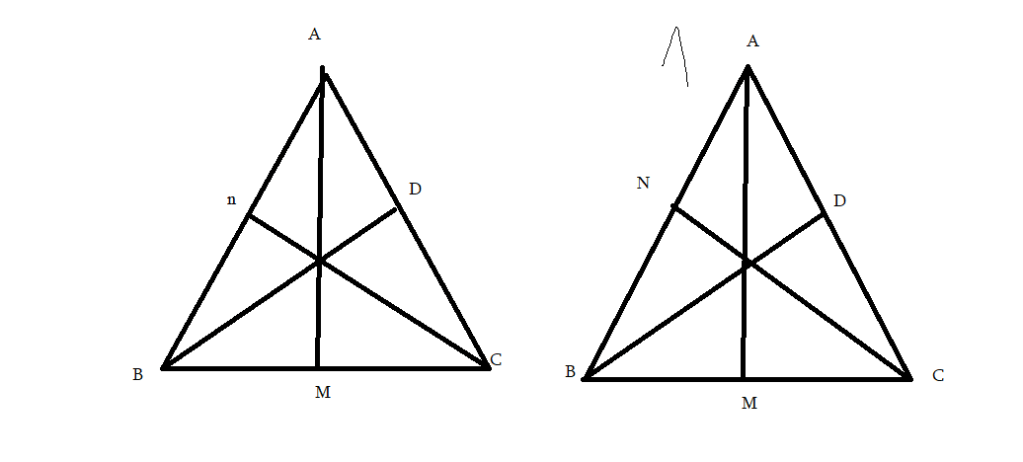
ա)Հայտնի է, որ BC = B1C1, <B = <B1 և <C = <C1

BC և B1C1 հատվածների առընթեր անկյուններն են <B և <C (եռանկյուն ABC-ի համար), <B1 և <C1 (եռանկյուն A1B1C1 — ի համար):

Ըստ եռանկյան երկրորդ հայտանիշի եռանկյունները հավասար են։

Եթե եռանկյունները հավասար են, այսինքն նրանց կողմերն էլ են հավասար։

CO և C1O1 հատվածները միջնագծեր են, այսինքն այդ հատվածները եռանկյունը բաժանել են երոկւ հավասար մասերի։

Ահա ապացուցելուց հետո կարելի է ասել, որ՝

եռանկյուն ACO = եռանկյուն A1C1O1

բ)ա տարբերակում պարզեցինք, որ երկու եռակյունները հավասար են, իսկ միջնակետը բաժանել է եռանկյունը երկու հավասար մասերի։

Եթե եռակյունը հավասար է մյուս եռանկյանը, այսինքն երկու մասերի բաժանելիս նրանք նույնպես հավասար կլինեն ինչպես՝եռանկյուն ACO = եռանկյուն A1C1O1։

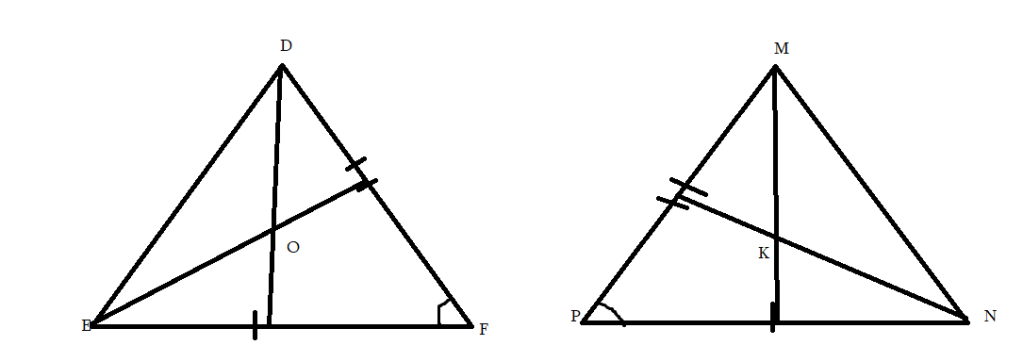
Հայտնի է, որ՝ EF = NP, DF = MP, <F = <P

Եթե ունենք այս պայմաննները կարող ենք ապացուցել, ըստ եռանկյան առաջին հայտանիշի, որ եռակյունները հավասար են։

Պարզեցինք, որ եռակյունները հավասար են։ Հիշացնում եմ, եթե եռանկյունները հավասար են, այսինքն կողմերը նույնպես իրար հավասար են։

Գիտենք, որ՝ ED = MN

Կիսորդները անկյունը բաժանում է երկու հավասար մասերի։

<N = <E, <D = <M

եռանկյուն DOE = եռանկյուն <MKN